Properties of parallelograms
One special kind of polygons is called a parallelogram. It is a quadrilateral where both pairs of opposite sides are parallel.
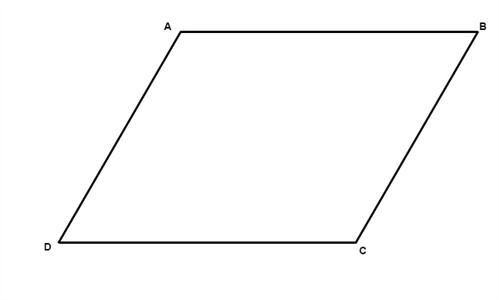
There are six important properties of parallelograms to know:
- Opposite sides are congruent (AB = DC).
- Opposite angels are congruent (D = B).
- Consecutive angles are supplementary (A + D = 180°).
- If one angle is right, then all angles are right.
- The diagonals of a parallelogram bisect each other.
- Each diagonal of a parallelogram separates it into two congruent triangles.
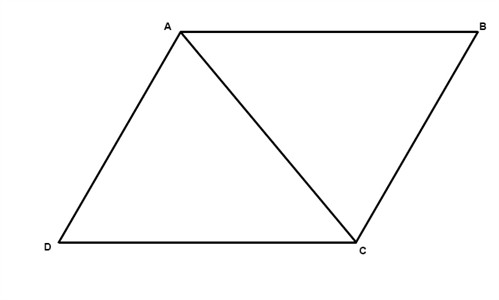
$$\triangle ACD\cong \triangle ABC$$
If we have a parallelogram where all sides are congruent then we have what is called a rhombus. The properties of parallelograms can be applied on rhombi.
If we have a quadrilateral where one pair and only one pair of sides are parallel then we have what is called a trapezoid. The parallel sides are called bases while the nonparallel sides are called legs. If the legs are congruent we have what is called an isosceles trapezoid.
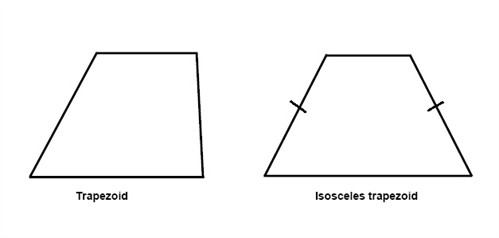
In an isosceles trapezoid the diagonals are always congruent. The median of a trapezoid is parallel to the bases and is one-half of the sum of measures of the bases.

$$EF=\frac{1}{2}(AD+BC)$$
Video lesson
Find the length of EF in the parallelogram
