More about triangles

The circumcenter of a triangle is the point that is at an equidistance from the vertices of the triangle. In the following triangle, D is the circumcenter of the triangle and therefore are AD = BD = CD

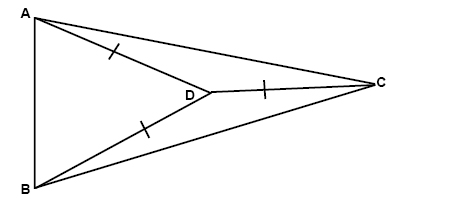
If we split an angle in a triangle in the absolute middle then that gives us a bisector of that angle. Any point on the bisector is equidistant from the sides of the angle:

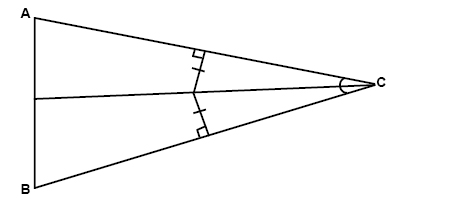
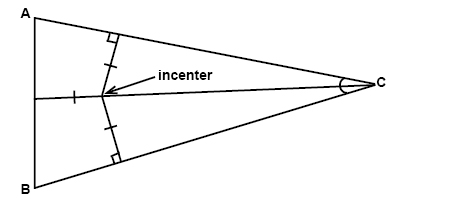
The point that is equidistant to all sides of a triangle is called the incenter:

A median is a line segment that has one of its endpoints in the vertex of a triangle and the other endpoint in the midpoint of the side opposite the vertex. The three medians of a triangle meet in the centroid. The centroid is located two thirds of the distance from any vertex of the triangle.

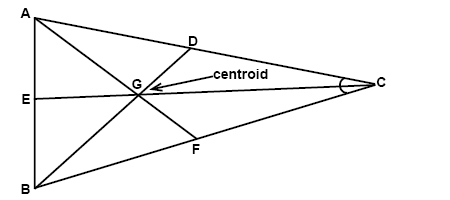
Here EG = (2/3)EC, FG = (2/3)FA, and DG = (2/3)DB.

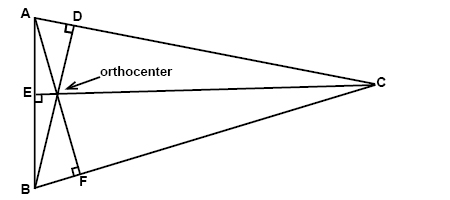
Every triangle has three altitudes. The altitude is a line segment that extends from a vertex and that is perpendicular to the side opposite the vertex. The intersection point of all three altitudes in a triangle is called the orthocenter:

---

Video lesson

Find the measure of the angles

$$\\\angle EBF\: and\: \angle FCB$$