Powers and exponents
We know how to calculate the expression 5 x 5. This expression can be written in a shorter way using something called exponents.
$$5\cdot 5=5^{2}$$
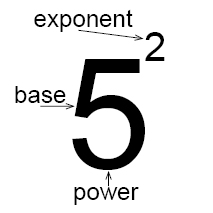
An expression that represents repeated multiplication of the same factor is called a power.
The number 5 is called the base, and the number 2 is called the exponent. The exponent corresponds to the number of times the base is used as a factor.
| 31 | 3 to the first power | 3 |
| 42 | 4 to the second power or 4 squared | 4 ∙ 4 |
| 53 | 5 to the third power or 5 cubed | 5 ∙ 5 ∙ 5 |
| 26 | 2 to the power of six | 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 |
Example
Write these multiplications like exponents
$$5\cdot 5\cdot 5=5^{3}$$
$$4\cdot 4\cdot 4\cdot 4\cdot 4=4^{5}$$
$$3\cdot 3\cdot 3\cdot 3=3^{4}$$
Multiplication
If two powers have the same base then we can multiply the powers. When we multiply two powers we add their exponents.
The rule:
$$x^{a}\cdot x^{b}=x^{a+b}$$
Example
$$4^{2}\cdot 4^{5}=\left ( 4\cdot 4 \right )\cdot \left ( 4\cdot 4\cdot 4\cdot 4\cdot 4 \right )=4^{7}=4^{2+5}$$
Division
If two powers have the same base then we can divide the powers. When we divide powers we subtract their exponents.
The rule:
$$\frac{x^{a}}{ x^{b}}=x^{a-b}$$
Example
$$\frac{4^{2}}{ 4^{5}}=\frac{{\color{red} {\not}{4}}\cdot {\color{red} {\not}{4}}}{{\color{red} {\not}{4}}\cdot {\color{red} {\not}{4}}\cdot 4\cdot 4\cdot 4}=\frac{1}{4^{3}}=4^{-3}=4^{2-5}$$
A negative exponent is the same as the reciprocal of the positive exponent.
$$x^{-a}=\frac{1}{x^{a}}$$
Example
$$2^{-3}=\frac{1}{2^{3}}$$
When you raise a product to a power you raise each factor with a power
$$(x\cdot y)^{a}=x^{a}\cdot y^{a}$$
Example
$$(2x)^{4}=2^{4}\cdot x^{4}=16x^{4}$$
The rule for the power of a power and the power of a product can be combined into the following rule:
$$(x^{a}\cdot y^{b})^{z}=x^{a\cdot z}\cdot y^{b\cdot z}$$
Example
$$(x^{3}\cdot y^{4})^{2}=x^{3\cdot 2}\cdot y^{4\cdot 2}=x^{6}\cdot y^{8}$$
Video lessons
Rewrite the expressions
$$2\cdot 2\cdot 2$$
$$x\cdot x\cdot x\cdot x\cdot x$$
$$3^{4}$$
$$x^{3}$$
Simplify the expression
$$\left ( x^{2}\cdot y^{3}\cdot z^{5} \right )^{3}$$
