Monomials and polynomials
A monomial is a number, a variable or a product of a number and a variable where all exponents are whole numbers. That means that
$$42, \: 5x, \: 14x^{12}, \: 2pq$$
all are examples of monomials whereas
$$4+y, \: \frac{5}{y}, \: 14^{x}, \: 2pq^{-2}$$
are not since these numbers don't fulfill all criteria.
The degree of the monomial is the sum of the exponents of all included variables. Constants have the monomial degree of 0.
If we look at our examples above we can see that
| Monomial | Degree |
| 42 | 0 |
| 5x | 0 + 1 = 1 |
| 14x12 | 0 + 12 = 12 |
| 2pq | 0 + 1 + 1 = 2 |
A polynomial as oppose to the monomial is a sum of monomials where each monomial is called a term. The degree of the polynomial is the greatest degree of its terms. A polynomial is usually written with the term with the highest exponent of the variable first and then decreasing from left to right. The first term of a polynomial is called the leading coefficient.
$$4x^{5}+2x^{2}-14x+12$$
Polynomial just means that we've got a sum of many monomials. If we have a polynomial consisting of only two terms we could instead call it a binomial and a polynomial consisting of three terms can also be called a trinomial.
We can add polynomials. We just add the like terms to combine the two polynomials into one.
Example
$$\left ( {\color{green} 4x^{2}+3x-14} \right )+\left ( {\color{blue} x^{3}-x^{2}+7x+1} \right )$$
Begin by grouping the like terms and then just simplify the expression
$${\color{blue} x^{3}}+\begin{pmatrix} {\color{green} 4x^{2}}{ \, -\,\color{blue} x^{2}} \end{pmatrix}+\begin{pmatrix} {\color{green} 3x}{\color{blue} \, +\, 7x} \end{pmatrix}+\begin{pmatrix} {\color{green} -14} {\color{blue} \, +\, 1} \end{pmatrix}=$$
$$=x^{3}+3x^{2}+10x-13$$
The same goes for subtracting two polynomials. Just subtract the like terms Or in other words add its opposites. Make the two polynomials into one big polynomial by taking away the parenthesis. Don't forget to reverse the signs within the second parenthesis since your multiplying all terms with -1.
$$\left ( {\color{green} {4x^{2}+3x-14}} \right )-\left ( {\color{blue} {x^{3}-x^{2}+7x+1}} \right )=$$
$$={\color{green} {4x^{2}+3x-14}}-{\color{blue} {x^{3}+x^{2}-7x-1}}$$
$$={\color{blue} {-x^{3}}}+\begin{pmatrix} {\color{green} {4x^{2}}}{\color{blue} {\, +\, x^{2}}} \end{pmatrix}+\begin{pmatrix} {\color{green} {3x}}{\color{blue} {\, -\, 7x}} \end{pmatrix}+\begin{pmatrix} {\color{green}{ -\, 14}}{\color{blue} {\, -\, 1}} \end{pmatrix}$$
$$=-x^{3}+5x^{2}-4x-15$$
Multiplication of polynomials is based on the distributive property.
$$x\cdot \left ( 2x^{2}+4x-3 \right )=x\cdot 2x^{2}+x\cdot 4x+x\cdot \left (-3 \right )=$$
$$=2x^{3}+4x^{2}-3x$$
When you multiply polynomials where both polynomials have more than one term you just multiply each of terms in the first polynomial with all of the terms in the second polynomial.
$$\begin{pmatrix} {\color{green} {4x^{2}+3x-14}} \end{pmatrix}\cdot \begin{pmatrix} {\color{blue} {7x+1}} \end{pmatrix}=$$
$${\color{green} {4x^{2}}}\begin{pmatrix} {\color{blue} {7x+1}} \end{pmatrix}{\color{green} {\, +\, 3x}}\begin{pmatrix} {\color{blue} {7x+1}} \end{pmatrix}{\color{green} \, -\, 14}\begin{pmatrix} {\color{blue} {7x+1}} \end{pmatrix}=$$
$$28x^{3}+4x^{2}+21x^{2}+3x-98x-14=$$
$$28x^{3}+25x^{2}-95x-14$$
When multiplying two binomial you can use the word FOIL to remember how to multiply the binomials. FOIL stands for First, Outer, Inner, Last.
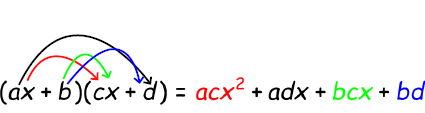
Video lesson
Simplify the following expression
$$4(x^{2}+x)-(x^{2}-4)$$
