Properties of equalities
Two equations that have the same solution are called equivalent equations e.g. 5 +3 = 2 + 6. And this as we learned in a previous section is shown by the equality sign =. An inverse operation are two operations that undo each other e.g. addition and subtraction or multiplication and division. You can perform the same inverse operation on each side of an equivalent equation without changing the equality.
$$5+3\, {\color{green} {-\, 2}}=6+2\, {\color{green}{ -\, 2}}$$
This gives us a couple of properties that hold true for all equations.
The addition property of equality tells us that adding the same number to each side of an equation gives us an equivalent equation
$$if\: a-b=c,then\: a-b\, {\color{green} {+\, b}}=c\, {\color{green} {+\, b}}, or \: a=c+b$$
The same goes with the subtraction property of equality.
$$if\: a+b=c,then\: a+b\, {\color{green} {-\, b}}=c\, {\color{green}{ -\, b}}, or \: a=c-b$$
As well as it goes for the multiplication property of equality. If you multiply each side of an equation with the same nonzero number you produce an equivalent equation.
$$if\: \frac{a}{b}=c, and\: b\neq 0,then\: \frac{a}{b}\, \cdot {\color{green} b}=c\cdot \, {\color{green} b}, or \: a=cb$$
And naturally this goes for the division property of equality as well. You can divide each side of an equation with the same nonzero number to produce an equivalent equation
$$if\: a\cdot b=c, and\: b\neq 0,then\: \frac{a\cdot b}{{\color{green} b}}\, =\frac{c}{{\color{green} b}}, or \: a=\frac{c}{b}$$
This gives us a way to change an equation to our own liking. Anything is acceptable as long as you do the same thing on both sides.
There are a couple of other properties of equations that can be good to know as well
Example
George has cut down a 60ft high oak tree. He now wants to chop it into smaller pieces. He first cuts it into two pieces that are both 30ft. And then he continues on into making ten pieces that all are 6ft long before loading them onto his truck.
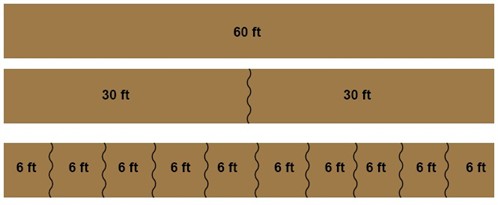
By looking at the different pieces of wood we can see that the following holds true.
$$60=30+30=6+6+6+6+6+6+6+6+6+6$$
This is called the reflexive property of equality and tells us that any quantity is equal to itself
$$a=a$$
We can also use this example with the pieces of wood to explain the symmetric property of equality. This property states that if quantity a equals quantity b, then b equals a.
$$if\: a=b, \: then\: b=a$$
Or if we use our example
$$if\: 60=30+30, \: then\: 30+30=60$$
Another property that can be explained by this is the transitive property of equality. It tells us that if a quantity a equals quantity b, and b equals the quantity, c, then a and c are equal as well.
$$if\: a=b\: and\: b=c, \: then\: a=c$$
Or in the numbers taken from the oak tree example
$$if\: 60=30+30$$
$$and\: 30+30=6+6+6+6+6+6+6+6+6+6$$
$$then\: 60=6+6+6+6+6+6+6+6+6+6$$
Since we know that 30 + 30 = 20 + 40 and that 30 + 30 = 60 we can substitute 30 + 30 for 20 + 40 and get 60 = 20 + 40. This is called the substitution property of equality.
If a = b, then a can be substituted for b in any expression.
Video lesson
Solve these equations using inverse operations
$$x + 8 = 10$$
$$x - 4 = 22$$
$$x\div 3 = 6$$
$$7x = 28$$
