The slope-intercept form of a linear equation
Earlier in this chapter we have expressed linear equations using the standard form Ax + By = C and also y= mx +b. Now we're going to focus on the slope-intercept form y = mx + b.
In the slope-intercept form you use the slope of the line and the y-intercept to express the linear function.
$$y=mx+b$$
Where m is the slope and b is the y-intercept.
Example
Graph the equation
$$y-2x=1$$
rewrite in slope-intercept form
$$y=2x+1$$
Identify the slope and the y-intercept
m = 2 and b = 1
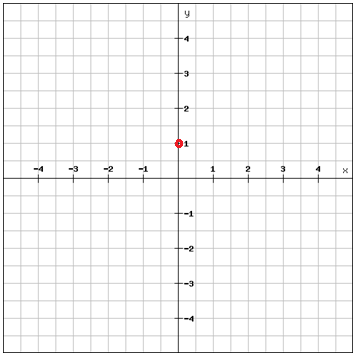
Plot the point corresponding to the y-intercept, (0,1)
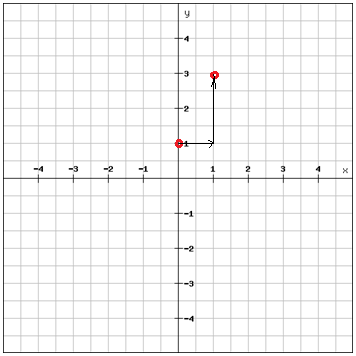
The m-value, the slope, tells us that for each step to the right on the x-axis we move 2 steps upwards on the y-axis (since m = 2)
And once you have your second point you can just draw a line through the two points and extend it in both directions.
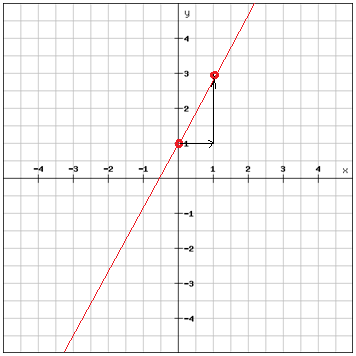
You can check to see that the line you've drawn is the correct one by substituting the coordinates of the second point into the original equation. If the equation holds true than the second point is correct.
Our second point = (1, 3)
$$y-2x=1$$
$$3-2\cdot 1=3-2=1$$
Our second point is a solution to the equation i.e. the line we drew is correct.
A line that passes through the origin has a y-intersect of zero, b = 0, and represents a direct variation.
$$y=mx$$
In a direct variation the nonzero number m is called the constant of variation.
You can name a function, f by using the function notion
$$f\left ( x \right )=mx+b$$
f(x) is another name for y and is read as "the value of f at x" or "f of x". You can use other letters than f to name functions.
A group of functions that have similar characteristics are called a family of functions. All functions that can be written on the form f(x) = mx + b belong to the family of linear functions.
The most basic function in a family of functions is called the parent function. The parent function of all linear functions is
$$f\left ( x \right )=x$$
Video lesson
Graph y = 3x - 2
