Solving absolute value equations and inequalities

The absolute number of a number a is written as

$\\ \left | a \right | \\$

And represents the distance between a and 0 on a number line.

An absolute value equation is an equation that contains an absolute value expression. The equation

$\\ \left | x \right |=a \\$

Has two solutions x = a and x = -a because both numbers are at the distance a from 0.

To solve an absolute value equation as

$\\ \left | x+7 \right |=14 \\$

You begin by making it into two separate equations and then solving them separately.

$\\\begin{matrix} x+7 =14: &x+7\, {\color{green} -\, 7}\, =14\, {\color{green} -\, 7} \\ & \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: x=7 \end{matrix} \\or\\\\ \begin{matrix} x+7 =-14: &x+7\, {\color{green} -\, 7}\, =-14\, {\color{green} -\, 7} \\ & \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: x=-21 \end{matrix}$

An absolute value equation has no solution if the absolute value expression equals a negative number since an absolute value can never be negative.

The inequality

$\\ \left | x \right |<2 \\$

Represents the distance between x and 0 that is less than 2

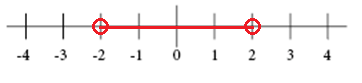
Whereas the inequality

$\\ \left | x \right |>2 \\$

Represents the distance between x and 0 that is greater than 2

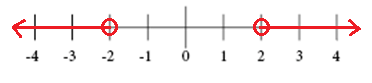
You can write an absolute value inequality as a compound inequality.

$\\ \left | x \right |<2\: or \\-2<x<2 \\$

This holds true for all absolute value inequalities.

$\\ \left | ax+b \right |<c,\: where\: c>0 \\=-c<ax+b<c \\\\ \left | ax+b \right |>c,\: where\: c>0 \\=ax+b<-c\: or\: ax+b>c \\$

You can replace > above with ≥ and < with ≤.

When solving an absolute value inequality it's necessary to first isolate the absolute value expression on one side of the inequality before solving the inequality.

Example:

Solve the absolute value inequality

$\\ 2\left |3x+9 \right |<36 \\\\\\\frac{2\left |3x+9 \right |}{2}<\frac{36}{2} \\\\\left | 3x+9 \right |<18 \\-18<3x+9<18 \\-18\, {\color{green} -\, 9}<3x+9\, {\color{green} -\, 9}<18\, {\color{green} -\, 9} \\-27<3x<9 \\\\\frac{-27}{{\color{green} 3}}<\frac{3x}{{\color{green} 3}}<\frac{9}{{\color{green} 3}} \\\\-9<x<3 \\$

Videolesson: Solve the absolute value equation

$\\4 \left |2x -1 \right | -2 = 10\\$

Next Class: Linear inequalitites, Linear inequalities in two variables

Download