Logarithm and logarithm functions
This is a very important section so ensure that you learn it and understand it. We will begin by drawing up a curve for y = 10x.
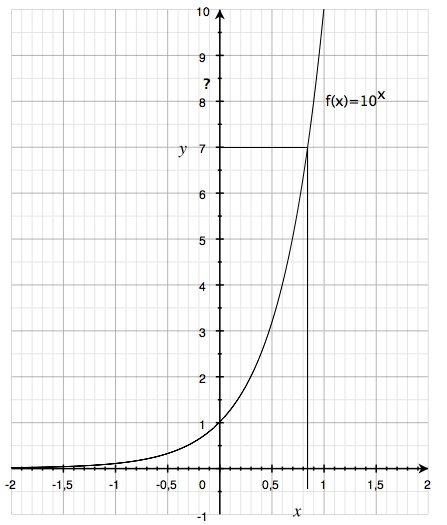
We have also marked the point where y = 7 on the curve. By reading the x-axis we see that when y = 7 then x ≈ 0.85. Thus:
$$10^{0,85}\approx 7$$
We can take whatever (positive) value on the y-axis and read it off on the x-axis. We can take whatever number and rewrite it as exponential expression where 10 is the base, i.e. as an exponent of 10.
Example
$$10^{0}=1\; \;\;\;\;\, \;10^{0.78}\approx 6\\ 10^{0.3}\approx2\; \;\; \;10^{0.85}\approx 7\\ 10^{0.48}\approx3\; \;\;10^{0.9}\approx 8\\ 10^{0.6}\approx4\; \;\;\;10^{0.95}\approx 9\\ 10^{0.7}\approx 5\; \;\;\;10^{1}=10$$
The exponent is known as a base 10 logarithm. For example, in order to solve equations such as:
$$11=10^{x}$$
we must either solve it graphically, by drawing up a 10x curve and find the value of x when y = 11 (as above); or we may use our pocket calculator that has a function which corresponds to manually drawing and reading of the graph. The key is designated as "lg" or "log". The solution to the equation is:
$$x=\log 11\approx 1.04$$
An equation of the form
$$y=log_{b}x$$
Is called a logarithmic function and when it is written as
$$y=log_{10}x$$
it is called base ten logarithm.
Video lesson
Base 10 logarithms
