Circular functions

The circle below is drawn in a coordinate system where the circle's center is at the origin and has a radius of 1. This circle is known as a unit circle.

The x and y coordinates for each point along the circle may be ascertained by reading off the values on the x and y axes. If you picture a right triangle with one side along the x-axis:

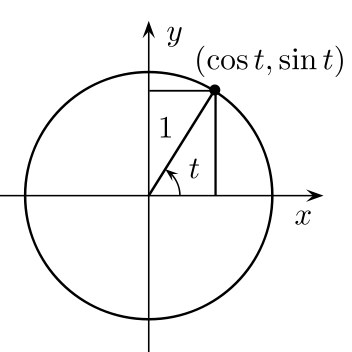
then the cosine of the angle would be the x-coordinate and the sine of the angle would be the y-coordinate. Since both the coordinates are defined by using a unit circle, they are often called circular functions.

Example

Solve the equation sin v = 0.5 with the unit circle.

If we examine the figure below, it is evident that there are two solutions to the problem:

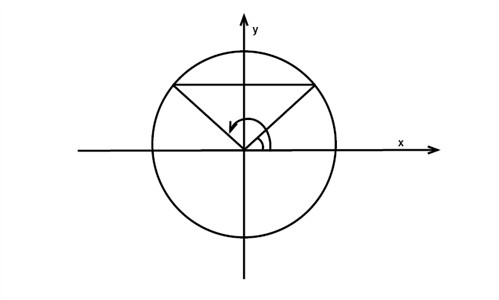
We arrive at the first solution by using a pocket calculator and keying:

$$v=\sin^{-1}0.5=30^{\circ}$$

Since half a revolution is 180 degrees, we ascertain the other angle by:

$$180-v=180-30=150^{\circ}$$

Video lesson

Solve the given equation using the unit circle Sin Ѳ = -1