Law of cosines

The law of cosines is a statement about a general triangle that relates the lengths of its sides to the cosine of one of its angles.

If we have the following triangel

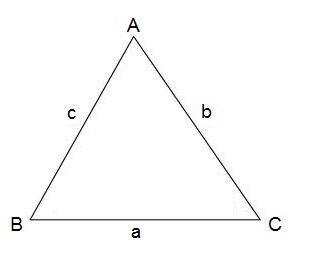
The following holds true

$$\\ a^{2}=b^{2}+c^{2}-2bc\: cos\: A\\ b^{2}=a^{2}+c^{2}-2ac\: cos\: B\\ c^{2}=a^{2}+b^{2}-2ab\: cos\: C\\$$

Example

If we have a triangle and we are given that C = 30° (this example is also shown in our video lesson) then find c if
a = 12 and b = 16.

To solve this we use the third equation and plug our values into it:

$$c^{2}=12^{2}+16^{2}-2\cdot 12\cdot 16\: cos\: 30^{\circ}$$

$$c^{2}\approx 67.446$$

$$c=\sqrt{67.446}=8.21$$

Video lesson

The example above in videoformat