Functions and linear equations
If we in the following equation y=x+7 assigns a value to x, the equation will give us a value for y.
Example
$$y=x+7$$
$$if\; x=2\; then$$
$$y=2+7=9$$
If we would have assigned a different value for x, the equation would have given us another value for y. We could instead have assigned a value for y and solved the equation to find the matching value of x.
In our equation y=x+7, we have two variables, x and y. The variable which we assign the value we call the independent variable, and the other variable is the dependent variable, since it value depends on the independent variable. In our example above, x is the independent variable and y is the dependent variable.
A function is an equation that has only one answer for y for every x. A function assigns exactly one output to each input of a specified type.
It is common to name a function either f(x) or g(x) instead of y. f(2) means that we should find the value of our function when x equals 2.
Example
$$f(x)=x+7$$
$$if\; x=2\; then$$
$$f(2)=2+7=9$$
A function is linear if it can be defined by
$$f(x)=mx+b$$
f(x) is the value of the function.
m is the slope of the line.
b is the value of the function when x equals zero or the y-coordinate of the point where the line crosses the y-axis in the coordinate plane.
x is the value of the x-coordinate.
This form is called the slope-intercept form. If m, the slope, is negative the functions value decreases with an increasing x and the opposite if we have a positive slope.
An equation such as y=x+7 is linear and there are an infinite number of ordered pairs of x and y that satisfy the equation.
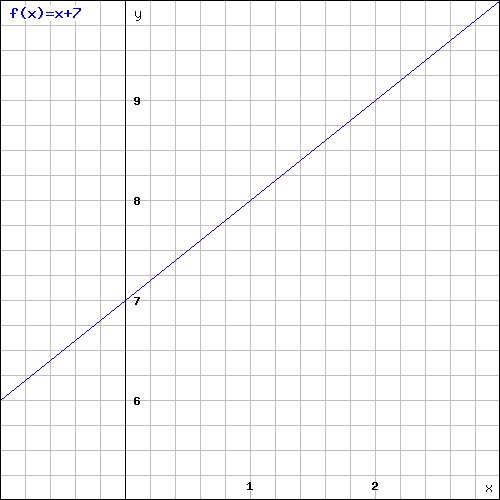
The slope, m, is here 1 and our b (y-intercept) is 7.
The slope of a line passing through points (x1,y1) and (x2,y2) is given by
$$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
$$x_{2}\neq x_{1}$$
If two linear equations are given the same slope it means that they are parallel and if the product of two slopes m1*m2=-1 the two linear equations are said to be perpendicular.
Video lesson
If x is -1 what is the value for f(x) when f(x)=3x+5?
