Law of cosines
The law of cosines is a statement about a general triangle that relates the lengths of its sides to the cosine of one of its angles.
If we have the following triangel
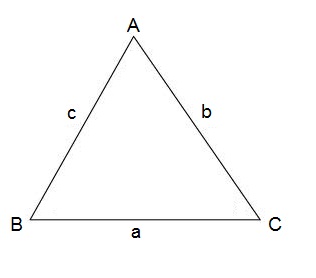
The following holds true
$$\\ a^{2}=b^{2}+c^{2}-2bc\: cos\: A\\ b^{2}=a^{2}+c^{2}-2ac\: cos\: B\\ c^{2}=a^{2}+b^{2}-2ab\: cos\: C\\$$
Example
If we have a triangle and we are given that C = 30° (this example is also shown in our video lesson) then find c if
a = 12 and b = 16.
To solve this we use the third equation and plug our values into it:
$$c^{2}=12^{2}+16^{2}-2\cdot 12\cdot 16\: cos\: 30^{\circ}$$
$$c^{2}\approx 67.446$$
$$c=\sqrt{67.446}=8.21$$
Video lesson
The example above in videoformat
