Law of sines

The law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles.

If we have the following triangel

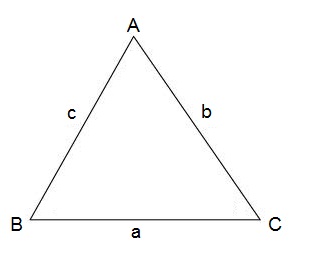
The following holds true

$$\frac{sin\; A}{a}=\frac{sin\; B}{b}=\frac{sin\; C}{c}$$

Example

If we have a triangle (this example is also shown in our video lesson) with one side that measure 2 with an opposite angle of 30° and one angle that is 40°. What is the measure of the side that is opposite to the angle that is 40°?

We use the law of sines to solve this problem:

$$\frac{sin\; 30^{\circ}}{2}=\frac{sin\; 40^{\circ}}{x}$$

$$x=2\cdot \frac{sin\; 40^{\circ}}{sin\: 30^{\circ}}=2.571$$

Video lesson

The example above in videoformat