The surface area and the volume of pyramids, prisms, cylinders and cones
The surface area is the area that describes the material that will be used to cover a geometric solid. When we determine the surface areas of a geometric solid we take the sum of the area for each geometric form within the solid.
The volume is a measure of how much a figure can hold and is measured in cubic units. The volume tells us something about the capacity of a figure.
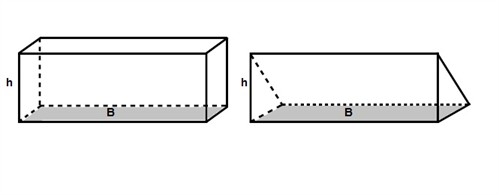
A prism is a solid figure that has two parallel congruent sides that are called bases that are connected by the lateral faces that are parallelograms. There are both rectangular and triangular prisms.
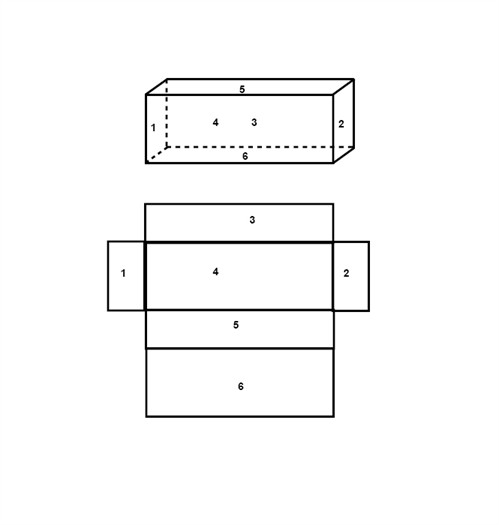
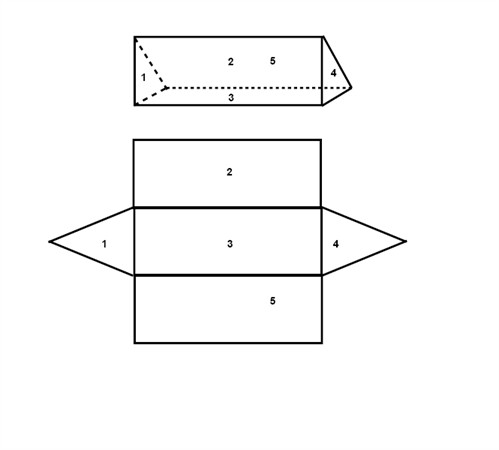
To find the surface area of a prism (or any other geometric solid) we open the solid like a carton box and flatten it out to find all included geometric forms.
To find the volume of a prism (it doesn't matter if it is rectangular or triangular) we multiply the area of the base, called the base area B, by the height h.
$$V=B\cdot h$$
A cylinder is a tube and is composed of two parallel congruent circles and a rectangle which base is the circumference of the circle.
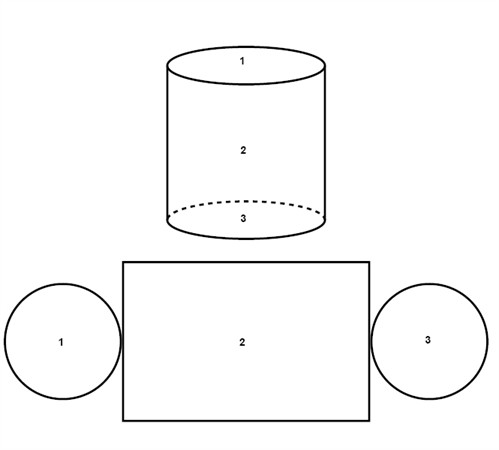
Example
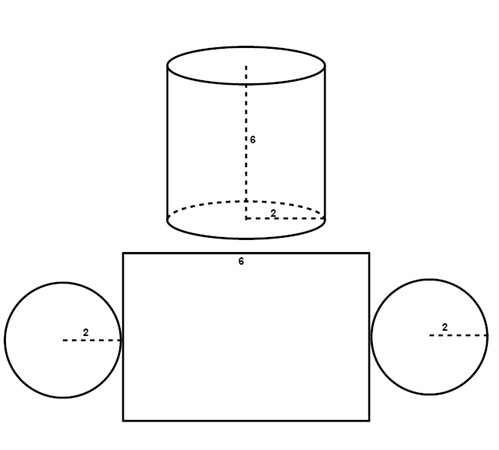
The area of one circle is:
$$A=\pi r^{2}$$
$$A=\pi \cdot 2^{2}$$
$$A=\pi \cdot 4$$
$$A\approx 12.6$$
The circumference of a circle:
$$C=\pi d$$
$$C=\pi \cdot 4$$
$$C\approx 12.6$$
The area of the rectangle:
$$A=C\cdot h$$
$$A=12.6 \cdot 6$$
$$A\approx 75.6$$
The surface area of the whole cylinder:
$$A=75.6+12.6+12.6=100.8\, units^{2}$$
To find the volume of a cylinder we multiply the base area (which is a circle) and the height h.
$$V=\pi r^{2}\cdot h$$
A pyramid consists of three, four or more (depending on the base) triangular lateral surfaces and a three or four sided surface, respectively, at its base. When we calculate the surface area of the pyramid below we take the sum of the areas of the 4 triangles area and the base square. The height of a triangle within a pyramid is called the slant height.
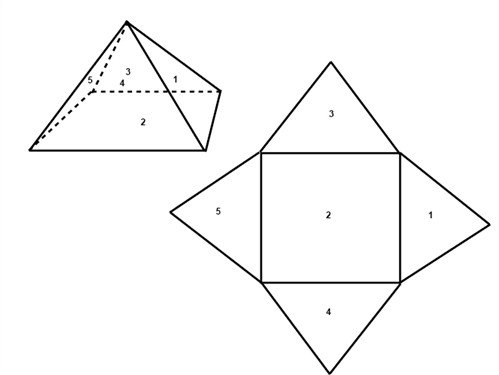
The volume of a pyramid is one third of the volume of a prism.
$$V=\frac{1}{3}\cdot B\cdot h$$
The base of a cone is a circle and that is easy to see. The lateral surface of a cone is a parallelogram with a base that is half the circumference of the cone and with the slant height as the height. This can be a little bit trickier to see, but if you cut the lateral surface of the cone into sections and lay them next to each other it's easily seen.
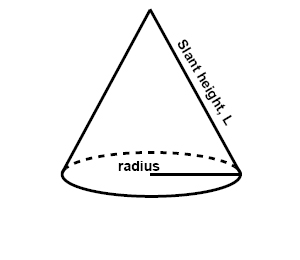
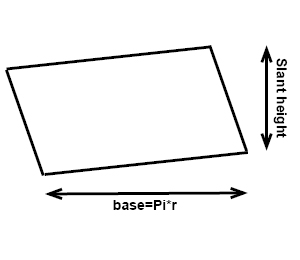
The surface area of a cone is thus the sum of the areas of the base and the lateral surface:
$$A_{base}=\pi r^{2}\: and\: A_{LS}=\pi rl$$
$$A=\pi r^{2}+\pi rl$$
Example
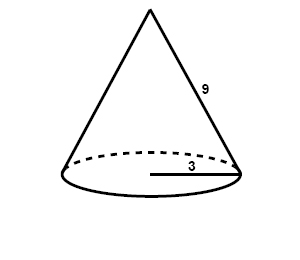
$$\begin{matrix} A_{base}=\pi r^{2}\: \: &\, \, and\, \, & A_{LS}=\pi rl\: \: \: \: \: \: \: \\ A_{base}=\pi \cdot 3^{2} & & A_{LS}=\pi \cdot 3\cdot 9\\ A_{base}\approx 28.3\: \: && A_{LS}\approx 84.8\: \: \: \: \: \\ \end{matrix}$$
$$A=\pi r^{2}+\pi rl=28.3+84.8=113.1\, units^{2}$$
The volume of a cone is one third of the volume of a cylinder.
$$V=\frac{1}{3}\pi \cdot r^{2}\cdot h$$
Example
Find the volume of a prism that has the base 5 and the height 3.
$$B=3\cdot 5=15$$
$$V=15\cdot 3=45\: units^{3}$$
Video lesson
Find the surface area of a cylinder with the radius 4 and height 8
Find the volume of a cone with height 5 and the radius 3
