Angles
It is common knowledge that the sum of the angles in a triangle is 180° but how about in polygons with a greater numbers of angles? If we are given a convex polygon with n sides and S is the sum of the measures of the interior angles then S = 180(n - 2).
Example
Find the sum of the measures of the interior angles in an octagon.
The octagon has 8 sides and we plug this value into our formula:
S = 180(8 - 2) = 1080°
Hence the sum of the measures of the interior angles in an octagon is 1080°.
Another thing with convex polygons is that the sum of the measures of the exterior angles is always 360°
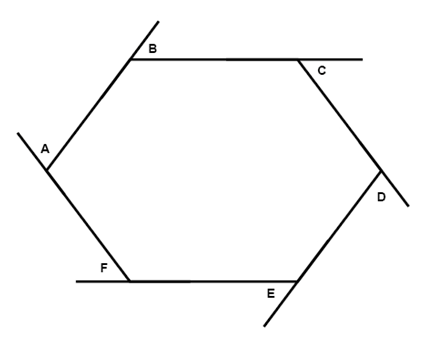
$$m\angle A+m\angle B+m\angle C+m\angle D+m\angle E+m\angle F=360$$
Video lesson
Find the sum of the measures of the interior angles in an hexagon
