Basic information about circles
A circle is all points in the same plane that lie at an equal distance from a center point. The circle is only composed of the points on the border. You could think of a circle as a hula hoop. It's only the points on the border that are the circle. The points within the hula hoop are not part of the circle and are called interior points.
The distance between the midpoint and the circle border is called the radius. A line segment that has the endpoints on the circle and passes through the midpoint is called the diameter. The diameter is twice the size of the radius. A line segment that has its endpoints on the circular border but does not pass through the midpoint is called a chord.
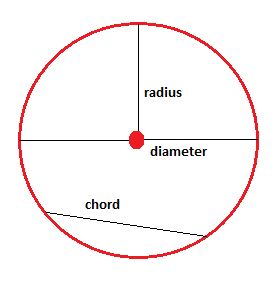
The distance around the circle is called the circumference, C, and could be determined either by using the radius, r, or the diameter, d:
$$C=2\pi r$$
$$C=\pi d$$
A circle is the same as 360°. You can divide a circle into smaller portions. A part of a circle is called an arc and an arc is named according to its angle. Arcs are divided into minor arcs (0° < v < 180°), major arcs (180° < v < 360°) and semicircles (v = 180°).
The length of an arc, l, is determined by plugging the degree measure of the Arc, v, and the circumference of the whole circle, C, into the following formula:
$$l=C\cdot \frac{v}{360}$$
When diameters intersect at the central of the circle they form central angles. Like when you cut a cake you begin your pieces in the middle.
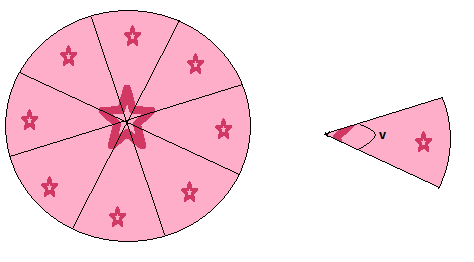
Example
As in the cake above we divide our circle into 8 pieces with the same angle. The circumference of the circle is 20 length units. Determine the length of the arc of each piece.
First we need to find the angle for each piece, since we know that a full circle is 360° we can easily tell that each piece has an angle of 360/8=45°. We plug these values into our formula for the length of arcs:
$$l=C\cdot \frac{v}{360}$$
$$l=20\cdot \frac{45}{360}=2.5$$
Hence the length of our arcs are 2.5 length units. We could even easier have told this by simply diving the circumference by the number of same size pieces: 20/8=2.5
Video lesson
What's the angle of the circle arc if we divide a cicle in \(8\) equally sized pieces
