Advanced information about circles

A line that intersects a circle in exactly one point is called a tangent and the point where the intersection occurs is called the point of tangency. The tangent is always perpendicular to the radius drawn to the point of tangency.

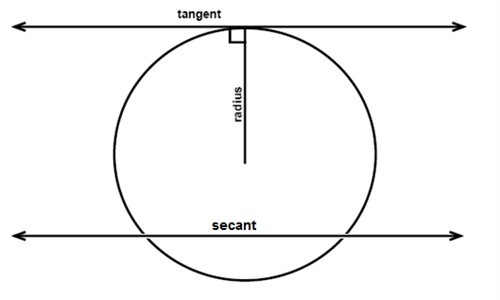
tangent radius secant

A secant is a line that intersects a circle in exactly two points.

When a tangent and a secant, two secants, or two tangents intersect outside a circle then the measure of the angle formed is one-half the positive difference of the measures of the intercepted arcs.

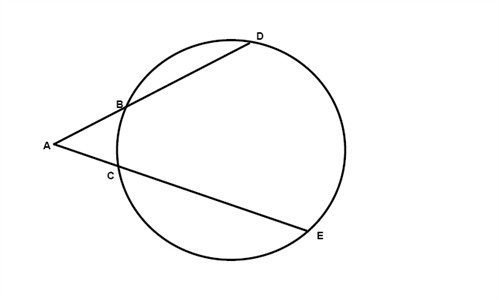
Circle Two Secants

$$m\angle A=\frac{1}{2}(m\overline{DE}-m\overline{BC} )$$

When two chords intersect inside a circle, then the measures of the segments of each chord multiplied with each other is equal to the product from the other chord:

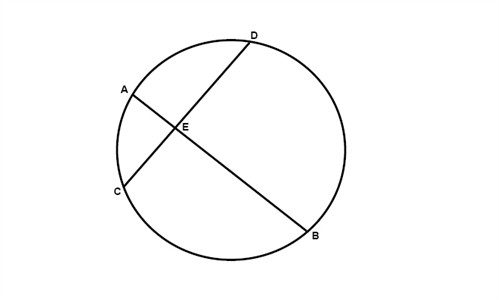
Circle Two Chords

$$AE\cdot EB=CE\cdot ED$$

If two secants are drawn to a circle from one exterior point, then the product of the external segment and the total length of each secant are equal:

Circle Two Secants

$$AB\cdot AD=AC\cdot AE$$

If one secant and one tangent are drawn to a circle from one exterior point, then the square of the length of the tangent is equal to the product of the external secant segment and the total length of the secant:

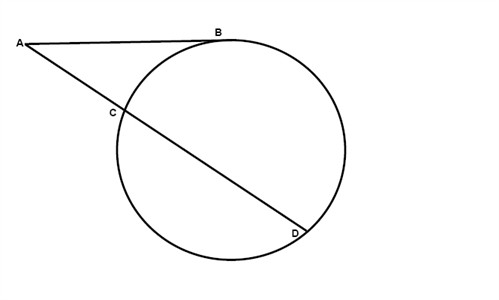
Circle Secant Tangent

$$AB^{2}=AC\cdot AD$$

If we have a circle drawn in a coordinate plane, with the center in (a,b) and the radius r then we could always describe the circle with the following equation:

$$(x-a)^{2}+(y-b)^{2}=r^{2}$$

Video lesson

Find the value of t in the figure