Inscribed angles and polygons

An inscribed angle is an angle that has its vertex on the circle and the rays of the angle are cords of the circle.

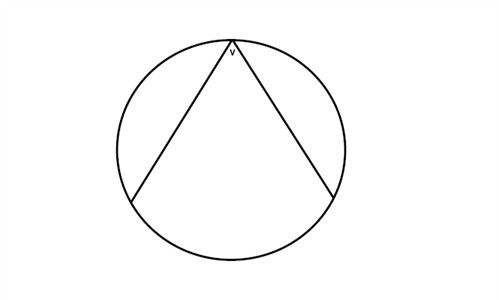
If we have one angle that is inscribed in a circle and another that has the same starting points but its vertex is in the center of the circle then the second angle is twice the angle that is inscribed:

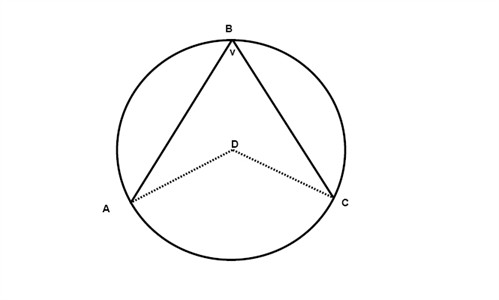
$$2\angle ABC=\angle ADC$$

Just as an angle could be inscribed into a circle a polygon could be inscribed into a circle as well:

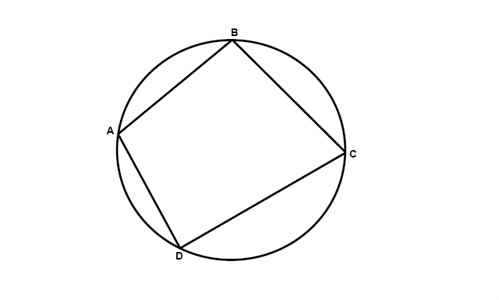
If a quadrilateral (as in the figure above) is inscribed in a circle, then its opposite angles are supplementary:

$$\angle A\; and\; \angle C\; are\; supplementary$$

$$\angle B\; and\; \angle D\; are\; supplementary$$

---

Video lesson

Find the value of the angle x in the figure.