Mean and geometry

The geometric mean is the positive square root of the product of two numbers.

Example

The geometric mean between 2 and 4 is x. The proportion 2:x=x:4 must be true hence

$$\frac{2}{x}=\frac{x}{4}$$

$$2\cdot 4=x^{2}$$

$$x^{2}=8$$

$$x=\sqrt{8}$$

If we in the following triangle draw the altitude from the vertex of the right angle then the two triangles that are formed are similar to the triangle we had from the beginning. The two triangles formed are also similar to each other.

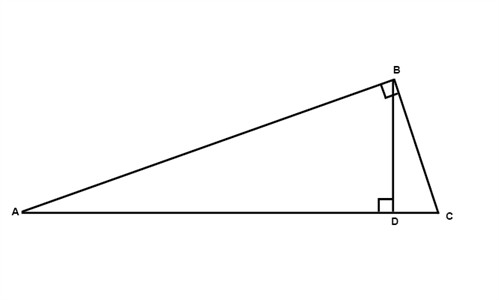
Altitude Right Triangle

$$\triangle ABC\sim \triangle BCD\sim\triangle ABD$$

The measure of the altitude drawn from the vertex of the right angle to the hypotenuse is the geometric mean between the measures of the two segments of the hypotenuse. Hence BD is the geometric mean of AD and DC.

Also in our figure the measure of a leg of the triangle is the geometric mean between the measures of the hypotenuse and the segment of the hypotenuse adjacent to that leg.

$$\frac{AC}{AB}=\frac{AB}{AD}\; and\; \frac{AC}{BC}=\frac{CB}{DC}$$

Video lesson

Find the value of x in the triangle.