Measure areas

The area of a parallelogram is measured in the same way as the area for a rectangle or a square. The height of a parallelogram is the distance between the two horizontal sides.

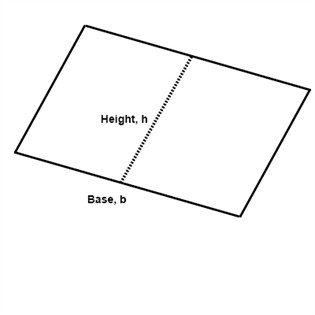
$\\A=b\cdot h\\$

Example:

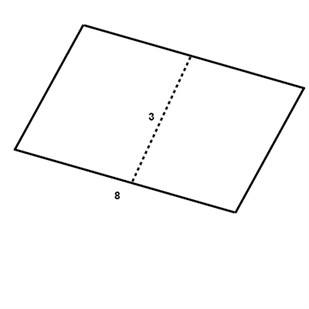
$\\\, A=b\cdot h\\ A=8\cdot 3 \\ A=24\: in^{2} \\$

As we showed in an earlier section we can divide a square or a quadrilateral into two triangles. This gives us that the area of a triangle is half the area of the quadrilateral with the same base and height.

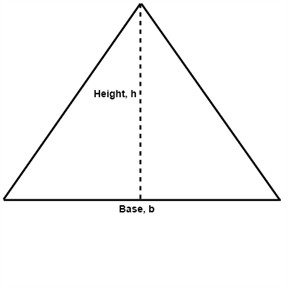
If the area of a parallelogram is A=b ∙ h then the area for a triangle is A=0.5b ∙h or

$\\ A=\frac{1}{2}b\cdot h\\$

Example:

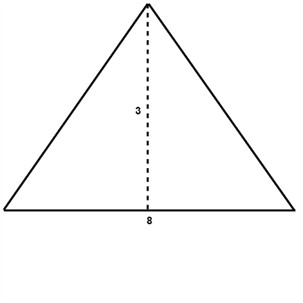
$\\ A=\frac{1}{2}b\cdot h\\\\\\ \: \: \: A=\frac{1}{2}\cdot 8\cdot 3 \\\\\\ A=\frac{1}{2}\cdot 24\\\\\\ \, A=12\: in^{2} \\$

A trapezoid is a quadrilateral with two parallel sides. Both parallel sides are called bases.

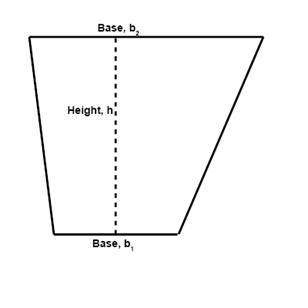
To find the area of a trapezoid we need to divide it into two triangles. Both triangles produced have the height h.

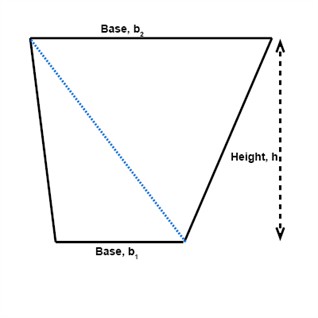
The area of the trapezoid is the sum of the areas of the two triangles.

$\\\begin{matrix} A_{1}=\frac{1}{2}b_{1}\cdot h & \: \: \:and \: \: &A_{2}=\frac{1}{2} b_{2}\cdot h \end{matrix} \\\\\\ A=\frac{1}{2}b_{1}\cdot h+\frac{1}{2} b_{2}\cdot h\\\\\\ \, A=\frac{1}{2}h\cdot (b_{1}+b_{2})\\$

Example:

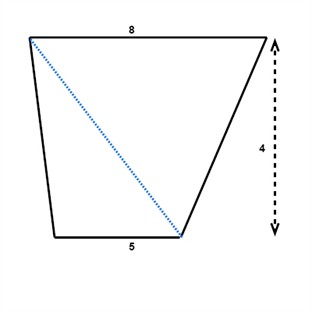
$\\ A=\frac{1}{2}\cdot 4\cdot (5+8)\\\\\\ A=2\cdot 13\\\\ A=26\, in^{2} \\$

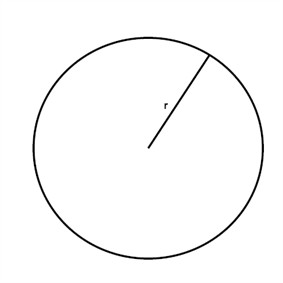
The area of a circle is different from the areas of a triangle or a quadrilateral. The area formula of a circle is:

$\\A=\pi r^{2}\\$

We get the area of a circle by multiplying π by the radius, r, squared.

Example:

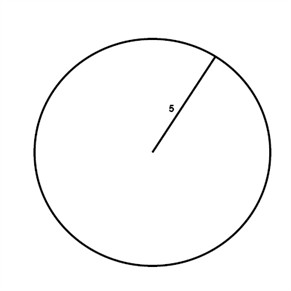
$\\A=\pi r^{2}\\ A=\pi \cdot 5^{2}\\ A=\pi \cdot 25\\ A\approx 75.5\, in^{2}\\$

Video lesson: Find the areas

Next Class: Area and Volume, Pyramids, prisms, cylinders and cones

Download