The Pythagorean Theorem

One of the best known mathematical formulas is Pythagorean Theorem, which provides us with the relationship between the sides in a right triangle. A right triangle consists of two legs and a hypotenuse. The two legs meet at a 90° angle and the hypotenuse is the longest side of the right triangle and is the side opposite the right angle.

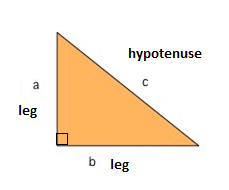
right triangle

The Pythagorean Theorem tells us that the relationship in every right triangle is:

$$a^{2}+b^{2}=c^{2}$$

Example

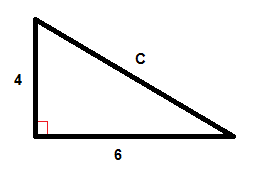
right triangle

$$C^{2}=6^{2}+4^{2}$$

$$C^{2}=36+16$$

$$C^{2}=52$$

$$C=\sqrt{52}$$

$$C\approx 7.2$$

There are a couple of special types of right triangles, like the 45°-45° right triangles and the 30°-60° right triangle.

right triangle

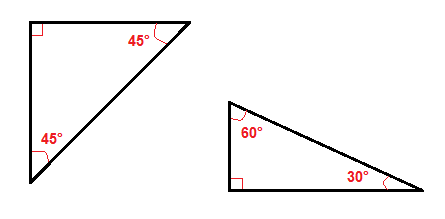
Because of their angles it is easier to find the hypotenuse or the legs in these right triangles than in all other right triangles.

In a 45°-45° right triangle we only need to multiply one leg by √2 to get the length of the hypotenuse.

Example

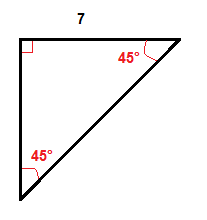
right triangle

We multiply the length of the leg which is 7 inches by √2 to get the length of the hypotenuse.

$$7\cdot \sqrt{2}\approx 9.9$$

In a 30°-60° right triangle we can find the length of the leg that is opposite the 30° angle by using this formula:

$$a=\frac{1}{2}\cdot c$$

Example

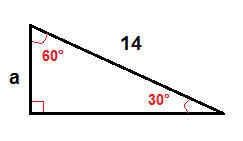
right triangle

To find a, we use the formula above.

$$a=\frac{1}{2}\cdot 14$$

$$a=7$$

Video lesson

Find the sides of this right triangle