Finding the greatest common factor

The greatest common factor is exactly as it sounds: the greatest factors of two or more numbers.

Example

Find the common factors for 60 and 30

Begin by factoring both numbers. Find all factors that the numbers have in common.

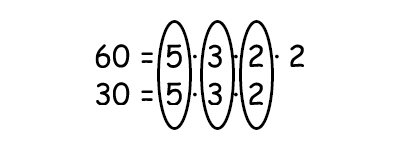
figure13

The product of all common factors is the greatest common factor (GCF)

$$5\cdot 3\cdot 2=30$$

The greatest common factor is 30

Example

You can also determine the GCF if you have both numbers and variables.

Find the common factors for 36x2y and 16xy

Factorize the numbers and identify all common factors. To get the GCF multiply all common factors.

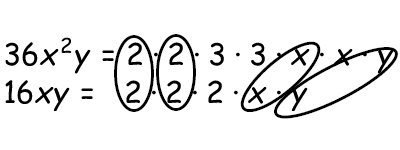
figure14

You can use the greatest common factor to simplify fractions.

A ratio is an expression that tells us the quotient of two numbers.

There are different ways to write a ratio and all examples below are read as "the ratio of 3 to 4".

$$3\: to\: 4$$

$$3:4$$

$$\frac{3}{4}$$

$$3\div 4$$

Example

You can simplify a ratio by findng the GCF

$$\frac{2000}{1500}$$

Fraction all numbers and find all common factors

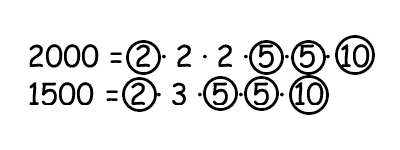
figure15

Multiply all common factors to find the GCF

$$2\cdot 5\cdot 5\cdot 10=500$$

Since the GCF is a factor of both the numerator and the denominator we can divide both the numerator and the denominator by the GCF to produce a simplified fraction.

$$\frac{2000\div 500}{1500\div 500}=\frac{4}{3}$$

Video lesson

Find the GCF of 24x3 and 56x3