Absolute value
In this section you'll learn how to the find the absolute value of integers.
4 - 0 = 4
4 - 1 = 3
4 - 2 = 2
4 - 3 = 1
4 - 4 = 0
4 - 5 = -1
In this pattern you can see that 4 - 5 is equal to a negative number. A negative number is a number that is less than zero (in this case -1). A negative number is always less than zero, 0.
We can study this in a diagram by using two examples: 0 - 4 = -4 and -1 - 3 = -4
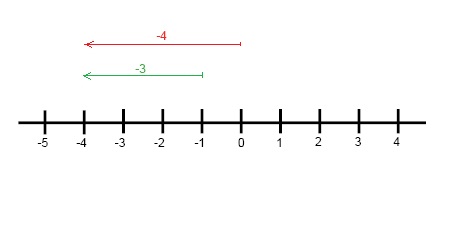
This kind of diagram is called a number line. There are some things that you need to observe when you draw and/or use a number line. Zero, is always in the middle and separates negative and positive numbers. On the left side of zero, you'll find numbers that are less than zero, the negative numbers. On the right side of zero, you'll find numbers that are greater than zero, the positive numbers. The absolute value is the same as the distance from zero of a specific number.
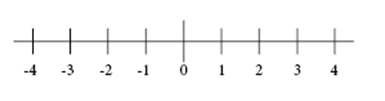
On this number line you can see that 3 and -3 are on the opposite sides of zero. Since they are the same distance from zero, though in opposite directions, in mathematics they have the same absolute value, in this case 3. The notation for absolute value is to surround the number by straight lines as in the examples below.
Example
Simplify the following expression
$$\left | 3 \right |+\left | -3 \right |=?$$
$$=3+3=6$$
Video lesson
Evaluate the following expression
$$\left | x \right |+11,\: \:\: x=-9$$
