Factorization and prime numbers

A factor is a number that is divisible by another number and where the quotient is an integer.

Example

$$\frac{18}{2}=9\Rightarrow factor$$

$$\frac{18}{4}=4.5\Rightarrow not\: a\: factor$$

2 is a factor of 18 because the answer is an integer (9). 4 is not a factor of 18 because the answer is 4 with a remainder of 5.

There are some rules of thumb to easily see if a number is a factor

2 - an even number is always divisible by two
3 - if the sum of its digits is divisible by 3
5 - if the last digit of the numerator is a 5 or 0 the number is divisible by 5
6 - if the number is divisible by 2 and 3
10 - if the last digit of the numerator is 0 the number is divisible by 10

Example

Determine whether 256 is divisible by 2, 3, 4, 5, 6, or 10

$$\begin{matrix} 256\div 2=128\: \: \: \: & ({\color{green} yes})\\ 256\div 3=85.3\: \: \: & ({\color{red} no})\: \: \\ 256\div 5=51.2 \: \: \: & ({\color{red} no})\: \: \\ 256\div 6=42.67 & ({\color{red} no})\: \: \\ 256\div 10=25.6\: & ({\color{red} no})\: \: \end{matrix}$$

A prime number is an integer greater than one that only has two factors (that it is divisible by), itself and 1 e.g. 2, 3, 5, 7, 11…

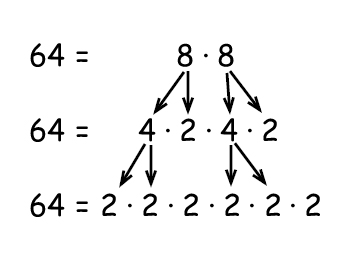
A composite number is an integer greater than one that has more than two factors e.g. the number 4 has the factors 1, 2, 4 and the number 6 has factors 1, 2, 3, 6. You can express a composite number in factors of prime numbers e.g. 4 = 2   2

The numbers 0 and 1 are considered neither composite numbers nor prime numbers.

Example

Video lesson

Factorize the expression

$$12x^{3}y^{2}$$