Trigonometry

The common three trigonometric ratios are sine, cosine and tangent which are defined by the following triangle:

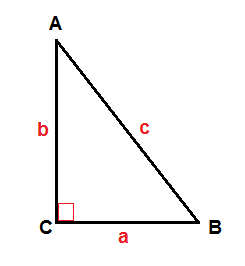
right triangle

abc show us the sides, ABC represent the angles.

$$Sine\, of\, A=\frac{measure\,of\,the\,leg\,opposite\,angle\,A}{measure\,of\,the\,hypotenuse}$$

$$\Rightarrow sin\left ( A \right )=\frac{a}{c}$$

$$Cosine\,of\,A=\frac{measure\,of\,the\,leg\,adjacent\,to\, angle\,A}{measure\,of\,the\,hypotenuse}$$

$$\Rightarrow cos\left ( A \right )=\frac{b}{c}$$

$$Tangent\, of\, A=\frac{measure\,of\,the\,leg\,opposite\,angle\,A}{measure\,of\,the\,leg\,adjacent\,to\,angle\,A}$$

$$\Rightarrow tan\left ( A \right )=\frac{a}{b}$$

Example

Find the sin(B), cos(B) and tan(B).

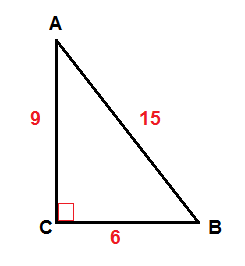
right triangle

$$Sine\, of\, B=\frac{measure\,of\,the\,leg\,opposite\,angle\,B}{measure\,of\,the\,hypotenuse}$$

$$Sin\, B=\frac{9}{15}=\frac{3}{5}=0.6$$

$$Cosine\,of\,B=\frac{measure\,of\,the\,leg\,adjacent\,to\, angle\,B}{measure\,of\,the\,hypotenuse}$$

$$Cos\, B=\frac{6}{15}=\frac{2}{5}=0.4$$

$$Tangent\, of\, B=\frac{measure\,of\,the\,leg\,opposite\,angle\,B}{measure\,of\,the\,leg\,adjacent\,to\,angle\,B}$$

$$Tan\, B=\frac{9}{6}=1.5$$

Video lesson

Find the measure of angle a in this right triangle