The slope of a linear function

The steepness of a hill is called a slope. The same goes for the steepness of a line. The slope is defined as the ratio of the vertical change between two points, the rise, to the horizontal change between the same two points, the run.

$$slope=\frac{rise}{run}=\frac{change\: in \: y}{change \: in\: x}$$

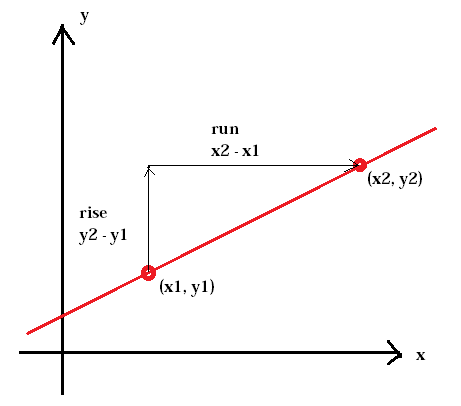
The slope of a line is usually represented by the letter m. (x₁, y₁) represents the first point whereas (x₂, y₂) represents the second point.

$$m=\frac{y_{2}\, -y_{1}}{x_{2}\, -x_{1}}$$

It is important to keep the x-and y-coordinates in the same order in both the numerator and the denominator otherwise you will get the wrong slope.

---

Example

Find the slope of the line

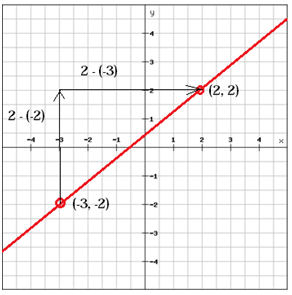
(x₁, y₁) = (-3, -2) and (x₂, y₂) = (2, 2)

$$m=\frac{y_{2}\, -y_{1}}{x_{2}\, -x_{1}}=\frac{2-\left ( -2 \right )}{2-\left ( -3 \right )}=\frac{2+2}{2+3}=\frac{4}{5}$$

A line with a positive slope (m > 0), as the line above, rises from left to right whereas a line with a negative slope (m < 0) falls from left to right.

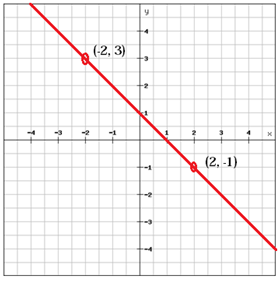
$$m=\frac{y_{2}\, -y_{1}}{x_{2}\, -x_{1}}=\frac{\left (-1 \right )-3}{2-\left ( -2 \right )}=\frac{-1-3}{2+2}=\frac{-4}{4}=-1$$

If two lines have the same slope the lines are said to be parallel.

---

You can express a linear function using the slope intercept form.

$$y=mx+b$$

$$m=slope$$

$$b=y - intercept$$

---

Video lesson

Find the slope