Multiplying polynomials and binomials

We can use the area of a rectangle to explain how you multiply a polynomial by a monomial.

---

Example

Find the area of this rectangle.

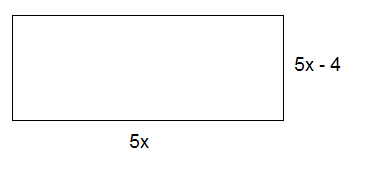
$$A=b\cdot h$$

$$A=5x\left ( 5x-4 \right ) \\A=5x\cdot 5x-5x\cdot 4$$

$$A=5\cdot 5\cdot x\cdot x-5\cdot 4\cdot x$$

$$A=25x^{2}-20x$$

---

This method is called the distributive property. The distributive property shows us how to write an expression in a different way.

$$a(b+c)=ab+ac$$

---

Example

With numbers

$$5\left (2+6 \right )=5\cdot 2+5\cdot 6=10+30=40$$

With variables and numbers:

$$7x+4x= x\left (7+4 \right )=11x$$

---

We can use the area of another rectangle to explain what happens when you multiply two binomials.

---

Example

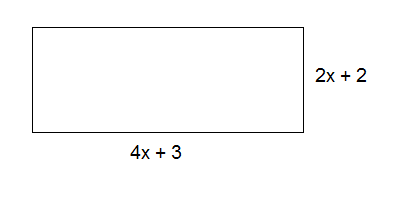
The area of the rectangle can be calculated by the use of the distributive property:

$$A=b\cdot h$$

$$A=({\color{red} {4x}}+{\color{blue} {3}})({\color{green} {2x}}+2)$$

$$A=({\color{red} {4x}}+{\color{blue} {3}})\cdot {\color{green} {2x}}+({\color{red} {4x}}+{\color{blue} {3}})\cdot 2$$

$$A={\color{red} {4x}}\cdot {\color{green} {2x}}+{\color{blue} {3}}\cdot {\color{green} {2x}}+{\color{red} {4x}}\cdot 2+{\color{blue} {3}}\cdot 2$$

$$A=8x^{2}+6x+8x+6$$

$$A=8x^{2}+14x+6$$

---

Video lesson

Expand the expression

$$(3x+4)(x^{2}-2)$$