Quadrilaterals, polygons and transformations
A quadrilateral is formed by four line segments that intersect at their endpoints. This quadrilateral is named by its endpoints, WXYZ, like a triangle. Squares and rectangles are quadrilaterals that have four right angles.
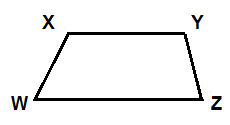
The sum of the angles of a quadrilateral is always 360°. Quadrilaterals can look very different:
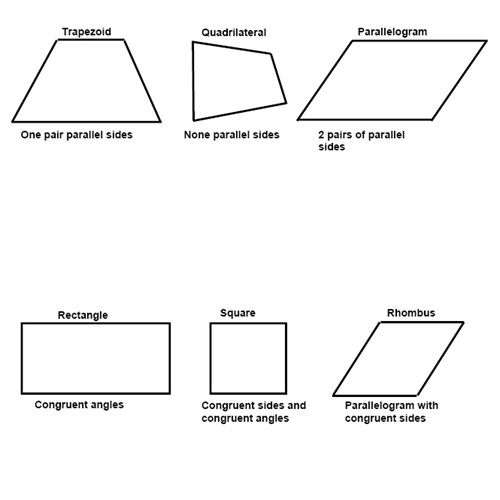
If two figures are similar to each other the corresponding angles are congruent and the corresponding sides are proportional.
Polygons are figures that are formed by three or more line segments. These line segments, even called sides, meet at their endpoints to form vertices.
If we compare the number of sides, diagonals and triangles of a quadrilateral a pentagon and a hexagon we can find a system between the different polygons.
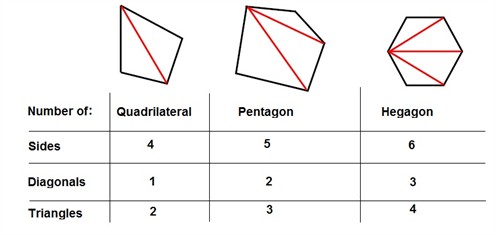
This can then help us find the sum of the measures of the angles in any polygon. If we compare the number of sides with the number of triangles, we see that there are always 2 less triangles than the number of sides. So, if a polygon has x sides, then the same polygon can form x - 2 triangles. The sum of the angles of a polygon is always
$$180^{\circ}\cdot \left ( x-2 \right )$$
Example
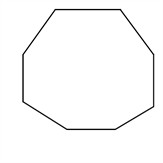
Find the measures of the angles in this octagon.
$$x=8$$
$$8-2=6$$
$$180^{\circ}\cdot (8-2)=$$
$$180\cdot 6^{\circ}=1080^{\circ}$$
The movement of geometric figures is called transformation. There are different types of transformations called translation, rotation and reflection.
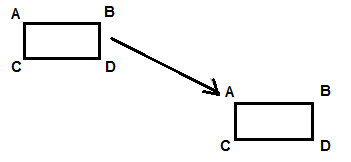
When you slide a figure in different ways, e.g. horizontally, vertically or both, it is called a translation.
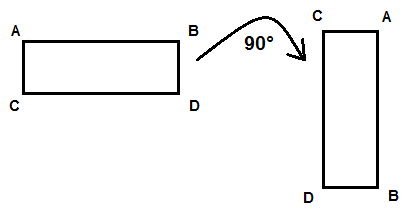
When you turn a figure around a specific point it is called rotation.
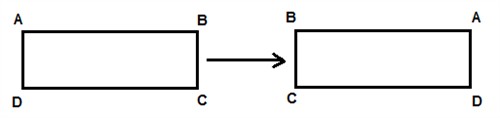
When you reverse a figure it is called a reflection.
Video lesson
Find the measures of angles of these figures
