Geometric sequences of numbers
A geometric sequence increase or decrease by a common factor - the common ratio.
Example
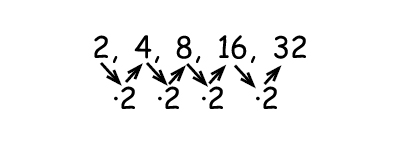
The common ratio is 2. We can write this as an algebraic expression.
$$a_{n}=a_{1}\cdot r^{n-1}$$
Where an is the first number (in this case 2).
r is the common factor (in this case 2).
n is the place in the set the number has (2 has n = 1, 8 has n = 3 etc.
We can rewrite this formula for our specific sequence:
$$a_{n}=2\cdot 2^{n-1}$$
If we would like to know the next number in the sequence after 32. The next number in the sequence is the 6th number. This gives us:
Example
$$a_{n}=a\cdot r^{n-1}$$
$$a_{6}=2\cdot 2^{6-1}$$
$$a_{6}=2\cdot 2^{5}$$
$$a_{6}=2\cdot 32$$
$$a_{6}=64$$
Video lesson
Find the eighth number
