Probability of events
Probability is a type of ratio where we compare how many times an outcome can occur compared to all possible outcomes.
$$Probability=\frac{The\, number\, of\, wanted \, outcomes}{The\, number \,of\, possible\, outcomes}$$
Example
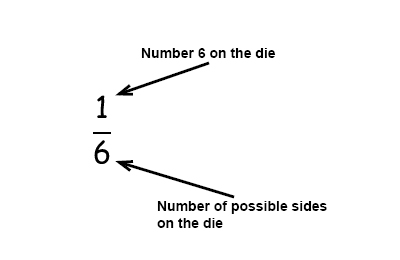
What is the probability to get a 6 when you roll a die?
A die has 6 sides, 1 side contain the number 6 that give us 1 wanted outcome in 6 possible outcomes.
Independent events: Two events are independent when the outcome of the first event does not influence the outcome of the second event.
When we determine the probability of two independent events we multiply the probability of the first event by the probability of the second event.
$$P(X \, and \, Y)=P(X)\cdot P(Y)$$
To find the probability of an independent event we are using this rule:
Example
If one has three dice what is the probability of getting three 4s?
The probability of getting a 4 on one die is 1/6
The probability of getting 3 4s is:
$$P\left ( 4\, and\, 4\, and\, 4 \right )=\frac{1}{6}\cdot \frac{1}{6}\cdot\frac{1}{6}=\frac{1}{216}$$
When the outcome affects the second outcome, which is what we called dependent events.
Dependent events: Two events are dependent when the outcome of the first event influences the outcome of the second event. The probability of two dependent events is the product of the probability of X and the probability of Y AFTER X occurs.
$$P(X \, and \, Y)=P(X)\cdot P(Y\: after\: x)$$
Example
What is the probability for you to choose two red cards in a deck of cards?
A deck of cards has 26 black and 26 red cards. The probability of choosing a red card randomly is:
$$P\left ( red \right )=\frac{26}{52}=\frac{1}{2}$$
The probability of choosing a second red card from the deck is now:
$$P\left ( red \right )=\frac{25}{51}$$
The probability:
$$P\left ( 2\,red \right )=\frac{1}{2}\cdot \frac{25}{51}=\frac{25}{102}$$
Two events are mutually exclusive when two events cannot happen at the same time. The probability that one of the mutually exclusive events occur is the sum of their individual probabilities.
$$P(X \, or \, Y)=P(X)+ P(Y)$$
An example of two mutually exclusive events is a wheel of fortune. Let's say you win a bar of chocolate if you end up in a red or a pink field.
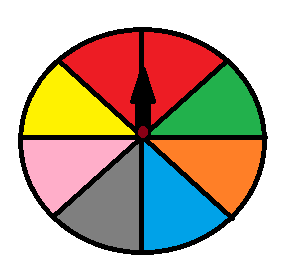
What is the probability that the wheel stops at red or pink?
P(red or pink)=P(red)+P(pink)
$$P\left (red \right )=\frac{2}{8}=\frac{1}{4}$$
$$P\left (pink \right )=\frac{1}{8}$$
$$P\left ( red\, or\, pink \right )=\frac{1}{8}+\frac{2}{8}=\frac{3}{8}$$
Inclusive events are events that can happen at the same time. To find the probability of an inclusive event we first add the probabilities of the individual events and then subtract the probability of the two events happening at the same time.
$$P\left (X \, or \, Y \right )=P\left (X \right )+ P\left (Y \right )-P\left (X \, and \, Y \right )$$
Example
What is the probability of drawing a black card or a ten in a deck of cards?
There are 4 tens in a deck of cards P(10) = 4/52
There are 26 black cards P(black) = 26/52
There are 2 black tens P(black and 10) = 2/52
$$P\left ( black\, or\, ten \right )=\frac{4}{52}+\frac{26}{52}-\frac{2}{52}=\frac{30}{52}-\frac{2}{52}=\frac{28}{52}=\frac{7}{13}$$
Video lesson
At Ann's 7-years olds party all 20 invited guests are going to get some candy from the fish pond. In 12 of the bags there is an extra chocolate bar. Tina and James are first and second out, what is the probability that they both get a bag with an extra chocolate bar?
