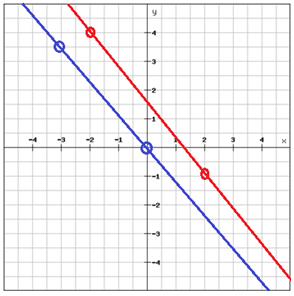
Parallel and perpendicular lines

If two non-vertical lines that are in the same plane has the same slope, then they are said to be parallel. Two parallel lines won't ever intersect.

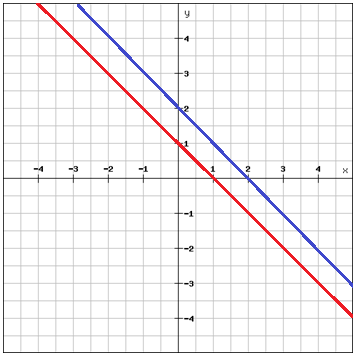
picture31

If two non-vertical lines in the same plane intersect at a right angle then they are said to be perpendicular. Horizontal and vertical lines are perpendicular to each other i.e. the axes of the coordinate plane.

Example

Compare the slope of the perpendicular lines

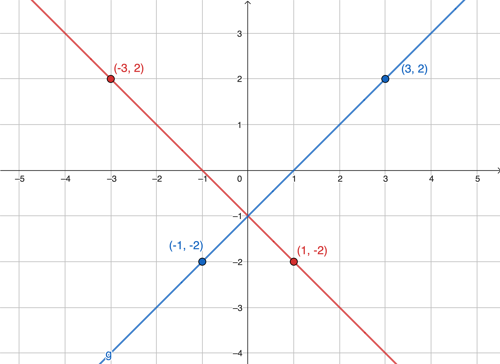
The slope of the red line:

$$m_{1}=\frac{-3-1}{2-( -2  )}=\frac{-4}{4}=-1$$

The slope of the blue line

$$m_{2}=\frac{2-\left ( -2 \right )}{3-\left ( -1 \right )}=\frac{4}{4}=1$$

The slopes of two perpendicular lines are negative reciprocals.

The product of the slopes of two perpendicular lines is -1 since

$$m\cdot -\frac{1}{m}=-1,\: \: where\: \: m_{1}=m\: \: and\: \: m_{2}=-\frac{1}{m}$$

Video lesson

Are these two line parallel?

picture33