Writing linear equations using the slope-intercept form
An equation in the slope-intercept form is written as
$$y=mx+b$$
Where m is the slope of the line and b is the y-intercept. You can use this equation to write an equation if you know the slope and the y-intercept.
Example
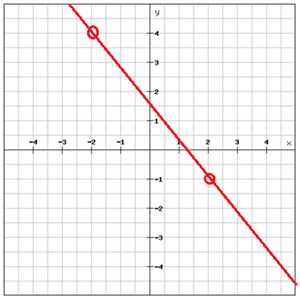
Find the equation of the line
Choose two points that are on the line
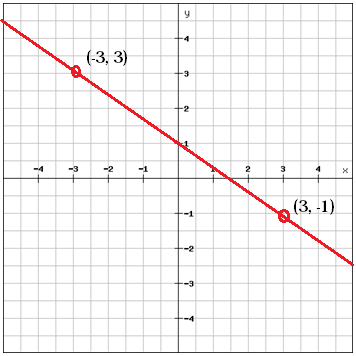
Calculate the slope between the two points
$$m=\frac{y_{2}\, -y_{1}}{x_{2}\, -x_{1}}=\frac{\left (-1 \right )-3}{3-\left ( -3 \right )}=\frac{-4}{6}=\frac{-2}{3}$$
We can find the b-value, the y-intercept, by looking at the graph
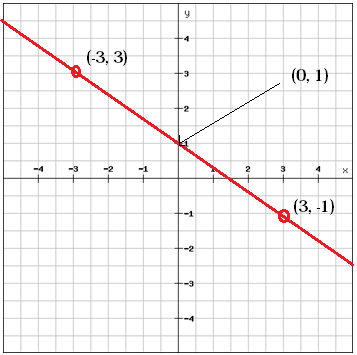
b = 1
We've got a value for m and a value for b. This gives us the linear function
$$y=-\frac{2}{3}x+1$$
In many cases the value of b is not as easily read. In those cases, or if you're uncertain whether the line actually crosses the y-axis in this particular point you can calculate b by solving the equation for b and then substituting x and y with one of your two points.
We can use the example above to illustrate this. We've got the two points (-3, 3) and (3, -1). From these two points we calculated the slope
$$m=-\frac{2}{3}$$
This gives us the equation
$$y=-\frac{2}{3}x+b$$
From this we can solve the equation for b
$$b=y+\frac{2}{3}x$$
And if we put in the values from our first point (-3, 3) we get
$$b=3+\frac{2}{3}\cdot \left ( -3 \right )=3+\left ( -2 \right )=1$$
If we put in this value for b in the equation we get
$$y=-\frac{2}{3}x+1$$
which is the same equation as we got when we read the y-intercept from the graph.
To summarize how to write a linear equation using the slope-interception form you
- Identify the slope, m. This can be done by calculating the slope between two known points of the line using the slope formula.
- Find the y-intercept. This can be done by substituting the slope and the coordinates of a point (x, y) on the line in the slope-intercept formula and then solve for b.
Once you've got both m and b you can just put them in the equation at their respective position.
Video lesson
Find the equation to the graph