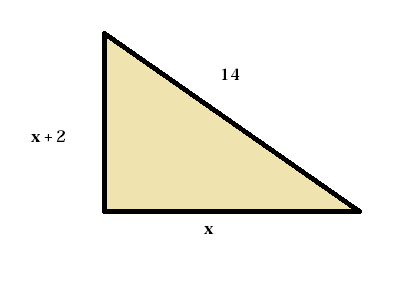The Pythagorean Theorem
One of the best known mathematical formulas is Pythagorean Theorem, which provides us with the relationship between the sides in a right triangle. A right triangle consists of two legs and a hypotenuse. The two legs meet at a 90° angle and the hypotenuse is the longest side of the right triangle and is the side opposite the right angle.
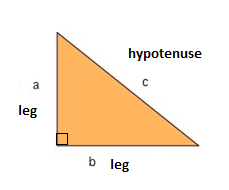
The Pythagorean Theorem tells us that the relationship in every right triangle is:
$$c^{2}=a^{2}+b^{2}$$
Example
Tom is about to buy a new tv. He wants to have a 42" television and wants to know how long the sides of the television are. Tom knows that that the television has the format of 16:9.
The format of 16:9 means that the width of the television is 16/9 of the height which gives us something like
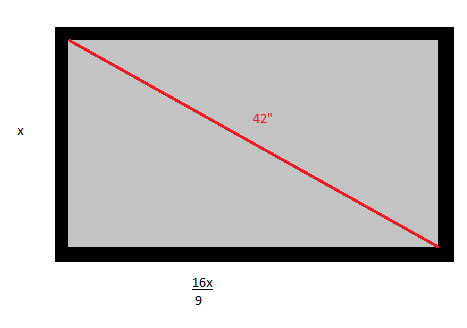
We can use the Pythagorean Theorem to solve x
$$x^{2}+\left ( \frac{16}{9}x \right )^{2}=42^{2}$$
$$x^{2}+\left ( \frac{16}{9} \right )^{2}\cdot x^{2}=1764$$
$$x^{2}\left ( 1+\frac{16^{2}}{9^{2}} \right )=1764$$
$$\frac{337}{81}x^{2}=1764$$
$$x^{2}=\frac{1764}{337\div 81}$$
$$\sqrt{x^{2}}=\sqrt{\frac{1764}{337\div 81}}$$
$$x\approx 20.6$$
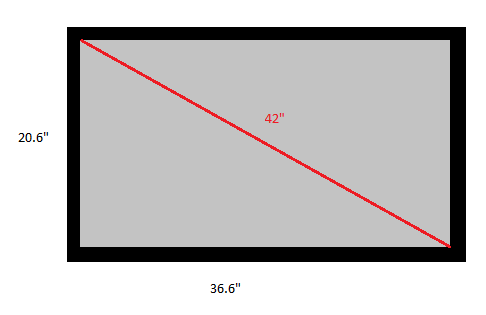
This gives us the height of the television which is 20.6". The width of television we get by
$$width=\frac{16}{9}\cdot x=\frac{16}{9}\cdot 20.6\approx 36.6$$
Which means that Tom's new television looks like this:
Video lesson
How long are the sides of the right triangle?