Division of polynomials
In the same way as multiplication was the same for rational expressions as for rational numbers so is the division of rational expressions the same as division of rational numbers. Remember that division of fractions of rational numbers is the same as multiplication by the reciprocal of the divisor.
Example
$$\frac{4x}{3}\div \frac{7y}{2}= \frac{4x}{3}\cdot \frac{2}{7y}=\frac{8x}{21y}$$
A polynomial divided by a monomial or a polynomial is also an example of a rational expression and it is of course possible to divide polynomials as well. When you divide a polynomial with a monomial you divide each term of the polynomial with the monomial.
Example
$$\frac{ax+b}{c}=\frac{ax}{c}+\frac{b}{c}$$
When you divide polynomials you may have to factor your polynomials to find a common factor between the numerator and the denominator
$$\frac{x^{2}-4x+3}{x-3}= $$
$$=\frac{\left ( x-3 \right )\left ( x-1 \right )}{x-3}=x-1$$
When there are no common factors between the numerator and the denominator or if you can't find the factors you can use a longer division process to simplify the expression.
Example
$$\frac{7x^{2}+x-8}{x-1}$$
You begin by dividing the first term of the dividend (7x2) with the first term of the divisor (x) to find the first term of the quotient (7x) and then you multiply the quotient term with the divisor and subtract.
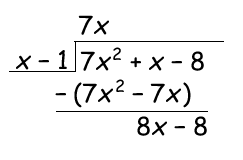
To find the next term of the quotient you just divide the first term of the remaining dividend (8x - 8) with the first term of the divisor (x)
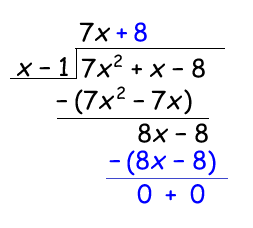
This means that:
$$\frac{7x^{2}+x-8}{x-1}=7x+8$$
