The graph of a radical function

A radical as you might remember is something that is under a radical sign e.g. a square root. A radical function contains a radical expression with the independent variable (usually x) in the radicand. Usually radical equations where the radical is a square root is called square root functions.

An example of a radical function would be

$$y=\sqrt{x}$$

This is the parent square root function and its graph looks like

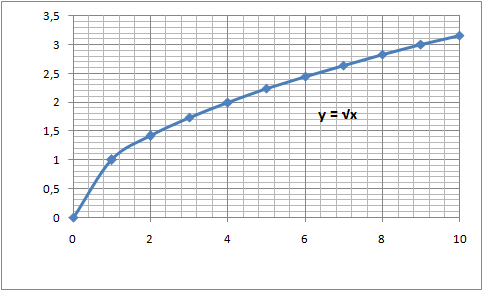
If we compare this to the square root function

$$y=a\sqrt{x}$$

We will notice that the graph stretches or shrinks vertically when we vary a

$$\begin{matrix} \left | a \right | >0\: \: \: \: \: \: \: & &\Rightarrow vertical\: stretch \\ 0<\left | a \right |<1 & & \Rightarrow vertical\: shrink\: \: \: \\ \end{matrix}$$

In the graph below we have radical functions with different values of a

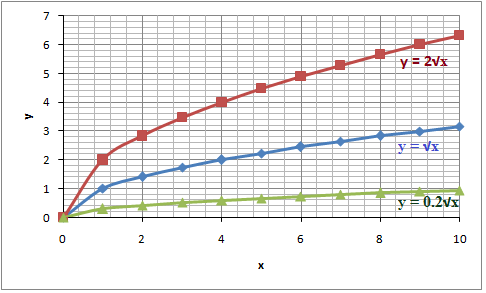
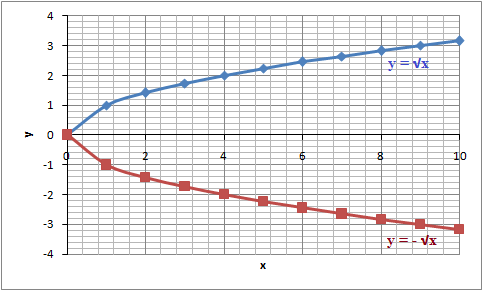
If a < 0 the graph

$$y=a\sqrt{x}$$

Is the reflection in the x-axis of the graph

$$y=\left |a \right |\sqrt{x}$$

Another square root equation would be

$$y=a\sqrt{x-b}+c$$

If you look at the graphs above which all have c = 0 you can see that they all have a range ≥ 0 (all of the graphs start at x=0 since there are no real solutions to the square root of a negative number). If you have a c ≠ 0 you'll have a radical function that starts in (0, c). An example of this can be seen in the graph below

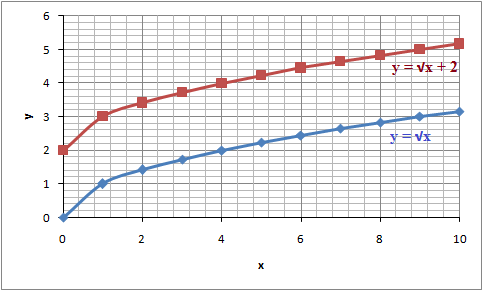
The value of b tells us where the domain of the radical function begins. Again if you look at the parent function it has a b = 0 and thus begin in (0, 0) If you have a b ≠ 0 then the radical function starts in (b, 0).

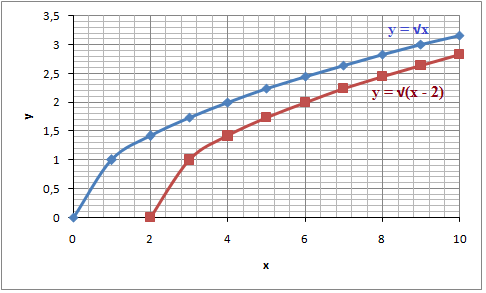
If both b ≠ 0 and c ≠ 0 then the radical function starts in (b, c)

---

Video lesson

Compare the radical functions

$$y_{1} =\sqrt{ x}$$

$$y_{2} = 3\sqrt{x}$$

$$y_{3} = \sqrt{x} + 2$$

$$y_{4} = \sqrt{x- 1}$$

$$y_{5} = \sqrt{x(x-2)} + 1$$