Solving linear inequalities
The graph of a linear inequality in one variable is a number line. Use an open circle for < and > and a closed circle for ≤ and ≥.
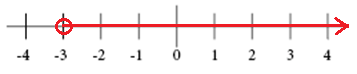
The graph for x > -3
The graph for x ≥ 2

Inequalities that have the same solution are called equivalent. There are properties of inequalities as well as there were properties of equality. All the properties below are also true for inequalities involving ≥ and ≤.
The addition property of inequality says that adding the same number to each side of the inequality produces an equivalent inequality
$$If \: x>y,\: then\: x+z>y+z$$
$$If\: x<y,\: then\: x+z<y+z$$
The subtraction property of inequality tells us that subtracting the same number from both sides of an inequality gives an equivalent inequality.
$$If \: x>y,\: then\: x-z>y-z$$
$$If\: x<y,\: then\: x-z<y-z$$
The multiplication property of inequality tells us that multiplication on both sides of an inequality with a positive number produces an equivalent inequality.
$$If \: x>y \: and\: z>0,\: then\: xz>yz$$
$$If\: x<y\: and\: z>0,\: then\: xz<yz$$
Multiplication in each side of an inequality with a negative number on the other hand does not produce an equivalent inequality unless we also reverse the direction of the inequality symbol
$$If \: x>y \: and\: z<0,\: then\: xz<yz$$
$$If\: x<y\: and\: z<0,\: then\: xz>yz$$
The same goes for the division property of inequality.
Division of both sides of an inequality with a positive number produces an equivalent inequality.
$$If \: x>y \: and\: z>0,\: then\: \frac{x}{z}>\frac{y}{z}$$
$$If\: x<y\: and\: z>0,\: then\: \frac{x}{z}<\frac{y}{z}$$
And division on both sides of an inequality with a negative number produces an equivalent inequality if the inequality symbol is reversed.
$$If \: x>y \: and\: z<0,\: then\: \frac{x}{z}<\frac{y}{z}$$
$$If\: x<y\: and\: z<0,\: then\: \frac{x}{z}>\frac{y}{z}$$
To solve a multi-step inequality you do as you did when solving multi-step equations. Take one thing at the time preferably beginning by isolating the variable from the constants. When solving multi-step inequalities it is important to not forget to reverse the inequality sign when multiplying or dividing with negative numbers.
Example
Solve the inequality
$$-2\left ( x+3 \right )<10$$
$$-2x-6<10$$
$$-2x-6\, {\color{green}{ +\, 6}<10\, }{\color{green} {+\, 6}}$$
$$-2x<16$$
$$\frac{-2x}{{\color{green}{ -2}}}\: {\color{blue} {>}}\: \frac{16}{{\color{green} {- 2}}}$$
$$x>-8$$
Video lesson
Solve the linear inequality
$$ -2\left (x+2 \right ) > 4 - x$$
