Use graphing to solve quadratic equations
In earlier chapters we've shown you how to solve quadratic equations by factoring. A quadratic equation as you remember is an equation that can be written on the standard form
$$ax^{2}+bx+c=0,\: \: where\: \: a\neq 0$$
You know by now how to solve a quadratic equation using factoring. Another way of solving a quadratic equation is to solve it graphically. The roots of a quadratic equation are the x-intercepts of the graph.
Example
Solve the equation
$$x^{2}-3x-10=0$$
Graph the equation. This could either be done by making a table of values as we have done in previous sections or by computer or a graphing calculator.
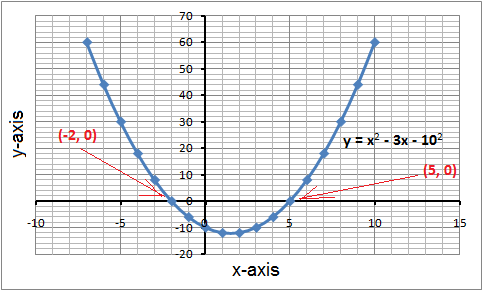
The parabola cross the x-axis at x = -2 and x = 5. These are the roots of the quadratic equation.
We can compare this solution to the one we would get if we were to solve the quadratic equation by factoring as we've done earlier.
$$x^{2}-3x-10=0$$
$$\left ( x+2 \right )\left ( x-5 \right )=0$$
$$x=-2\: \: or\: \: x=5$$
- A quadratic equation has two roots if its graph has two x-intercepts
- A quadratic equation has one root it its graph has one x-intercept
- A quadratic equation has no real solutions if its graph has no x-intercepts.
Here you can get a visual of your quadratic function
Worksheets
If you want to practice finding the roots of the graph of a quadratic functions we have some worksheets with answers for you.
Video lesson
Solve the equation graphically
$$x^{2}-3x-10=0$$
